Revolutionary Deep Learning Approaches for Massive MIMO Systems

Corresponding Author: Prof. Ertuğrul Başar, Koç University (ebasar@ku.edu.tr)

---

You can cite this article with the following:

---

Abstract

Multiple-input multiple-output (MIMO) technology has been widely utilized in current fourth-generation (4G) networks, also known as the Long Term Evolution (LTE). In comparison to 4G, emerging fifth-generation (5G) and beyond cellular communication technologies need far more compelling requirements for spectral efficiency, data rate, and latency. Therefore, massive MIMO appears as a groundbreaking technology with large-scale antenna arrays deployed at base stations, which dramatically enhances the benefits of conventional MIMO systems. However, massive MIMO technology comes with the expense of challenging constraints that leave the existing communication and signal processing theory-based concepts desperate. At this point, deep learning (DL) demonstrates immense promise with the mapping capability from input features to desired labels using neural networks (NN). In this article, we reveal the advancements of massive MIMO systems, highlight limitations that are challenging to overcome with traditional methods, and shed light on emerging DL applications in massive MIMO systems. This introductory article has been adopted from [1].

Introduction

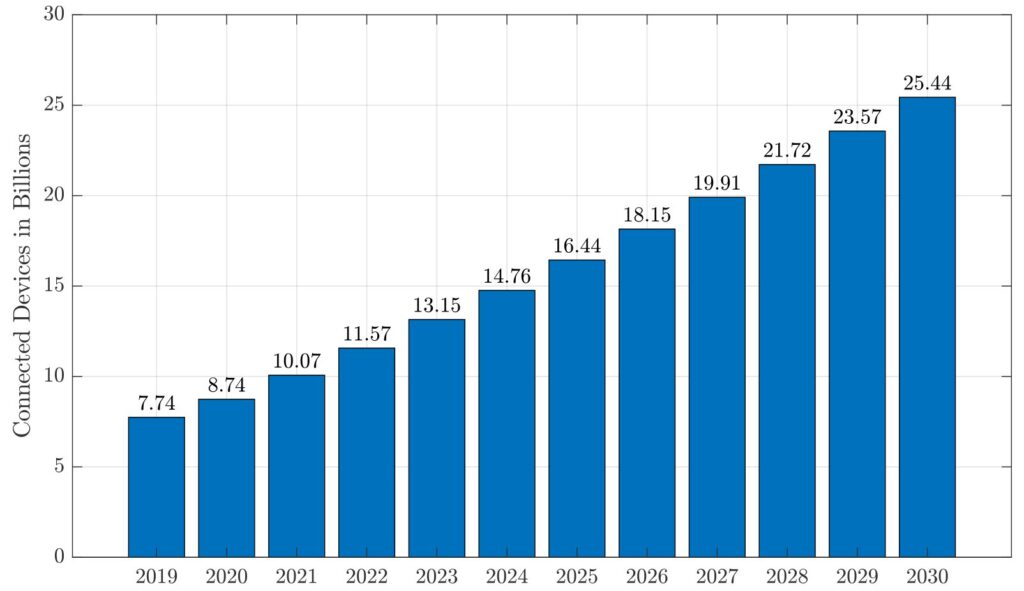
Wireless communication technologies have been evolving since the first generation (1G) of cellular networks emerged in the 1980s. The most recent fifth-generation (5G) of cellular communication technology, starting with the 3GPP (3rd Generation Partnership Project) Release 15 standard [2], electrifies both the academic world and the mobile market. The proliferation of cellular networks has resulted in a remarkable increase in internet-of-things (IoT) devices and their interconnection. According to Statista [3], the total number of connected IoT devices is estimated to rise from 8.74 billion in 2020 to 16.44 billion by 2025, representing an almost 88% growth, as given in Fig. 1.

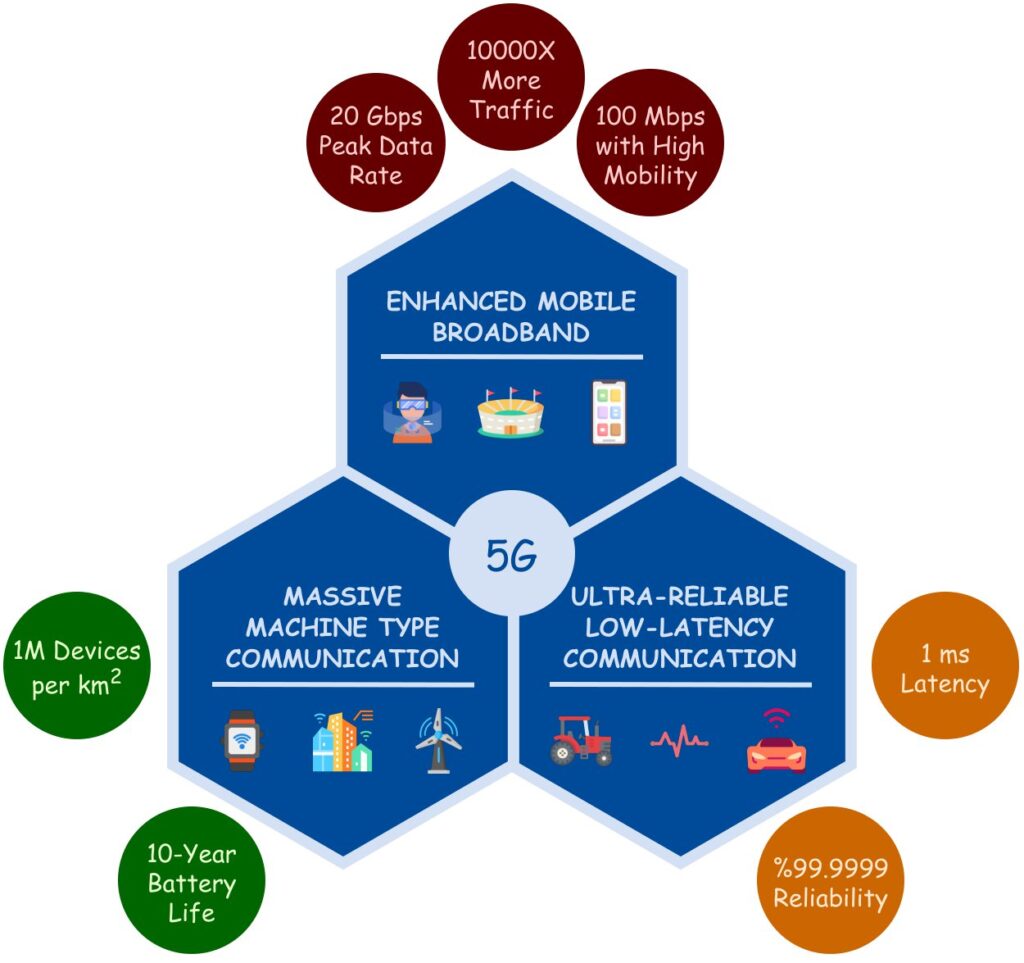
This development in the connection of IoT devices enables thrilling applications in 5G, such as autonomous cars and virtual reality. The International Telecommunication Union (ITU) has classified 5G applications into three categories: enhanced mobile broadband (eMBB) services, massive machine-type communications (mMTC), and ultra-reliable and low-latency communications (URLLC) [4], [5], [6]. Although these use cases have different requirements, 5G is expected to support high data rates, reduced latency in data transmission, energy efficiency, strong data security, and high scalability for a multitude of devices [4], as given in Fig. 2.

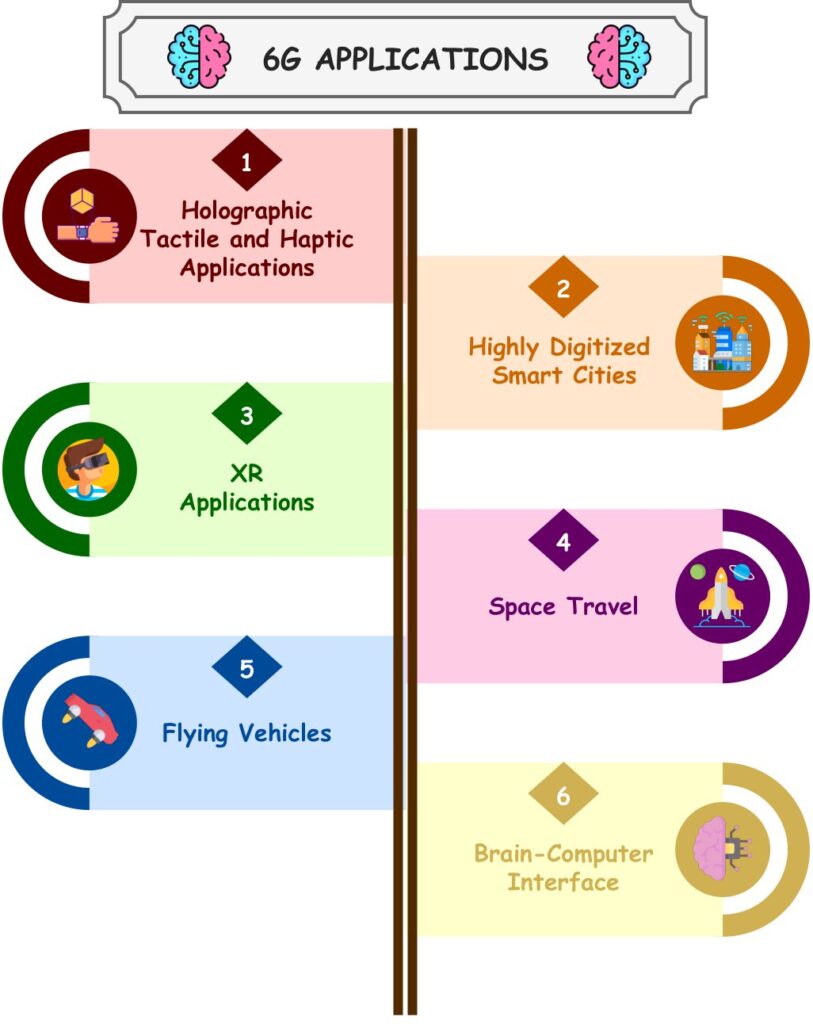
Even though 5G has shown significant promise for a globally connected wireless world, it has been questioned whether 5G can be the actual facilitator of the internet-of-everything (IoE) [7]. As given in Fig. 1, the forecasted IoT device connection will be 25.44 billion in 2030, which indicates that the necessities of a fully-intelligent information society beyond 2030 are considerably rigorous [1]. Therefore, communication researchers have already started scrutinizing novel communication technologies for the sixth generation (6G) of the wireless world to overcome the drawbacks of 5G and build an outstanding wireless future. The thrilling applications expected to come into life with 6G, such as haptic technology, brain-computer interface, truly immersive virtual reality, and space travel provided in Fig. 3, will introduce compelling requirements. Therefore, researchers have developed innovative physical layer (PHY) communication solutions.

PHY of a wireless system, also known as Layer-1, is the initial layer of the network that deals with data transmission over the air. The transmitter side of a PHY communication transforms information bits into baseband electric pulses located around 0 Hz. These pulses are then converted to electromagnetic waves called radio-frequency (RF) signals by modulating a carrier signal’s phase, amplitude, or both with a higher operating frequency [9]. The operating frequency of a carrier signal is standard-specific. The technical specifications of the 5G PHY, commonly known as New Radio (NR) L1, are defined by the 3GPP organization [10]. The receiver side follows the reverse procedure of the transmitter and decodes received RF signals into information bits. The signal processing conducted to convert information bits to symbols and to prepare symbols for the fading and disruptive transmission effects significantly impacts the quality of a PHY transmission. Therefore, wireless researchers have been studying improving transmission reliability, increasing the number of bits transmitted in a channel use, and enhancing data security through novel PHY techniques. The existing model-based signal processing techniques rely on mathematically optimized models such as communication and information theory. These strong theoretical models individually optimize each signal processing block of a PHY transmission, such as bit modulation and channel estimation. However, the critical question is:

Does separate block optimization guarantee end-to-end (E2E) optimization?

In this article, we pave the way for a solid answer to this question. In particular, we investigate deep learning (DL) solutions for massive multiple-input multiple-output (MIMO) systems. DL models are composed of neural networks (NN) with learnable parameters. DL methods have already proved their success in diverse fields, including natural language processing, speech recognition, and computer vision, where it is incredibly challenging to create a theoretical model for mapping the input features to the desired labels [1]. However, their applicability to existing signal processing techniques has remained limited thus far [1], [11]. Since the traditional PHY structure is optimized on a block-by-block basis, DL must go beyond strict boundaries to replace traditional model-based approaches. Our primary motivation is to shed light on the potential of DL methods in ensuring the E2E optimization of a PHY transmission. The most noteworthy innovation in 6G is the replacement of individually optimized signal processing units in a PHY architecture with a gigantic DL network that enables E2E optimization. We call this drastic paradigm shift from block-optimized model-based structure to E2E-optimized intelligent design the PHY revolution. In what follows, we will briefly explain the details and advantages of massive MIMO systems.

Massive MIMO: Extending to the Spatial Domain

In a MIMO system model, both transmitter and receiver are equipped with multiple antennas, as given in Fig. 4.

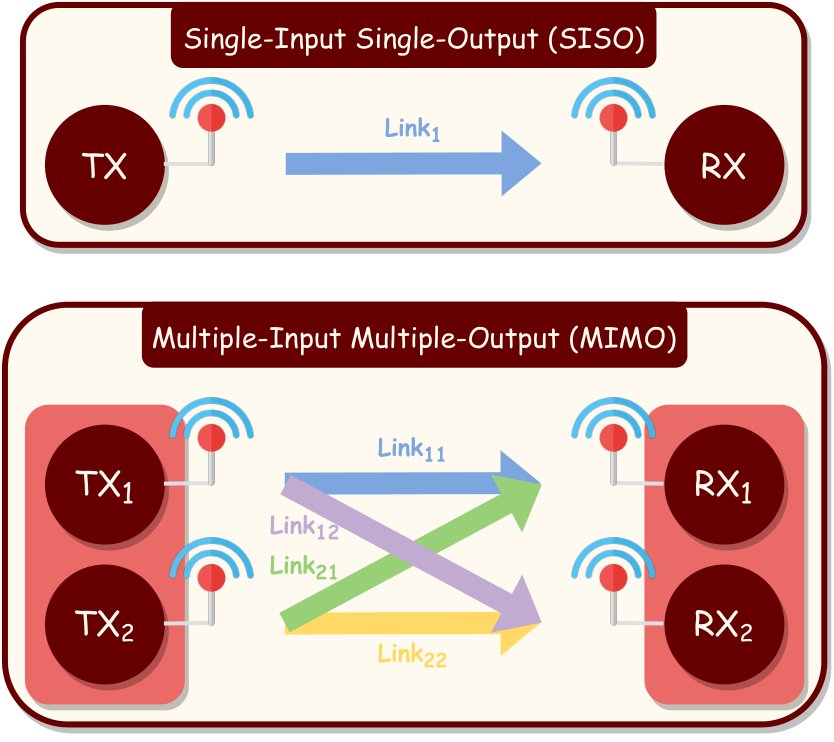
In addition to time and frequency domains, multiple antennas introduce a third resource dimension: the spatial domain [12]. Using multiple antennas at both ends delivers substantial benefits compared to a single transmission link. Assuming a MIMO system with \(N_{T}\) transmit and \(N_{R}\) receive antennas, these benefits are described below:

Spatial Diversity Gain

The wireless transmission link between a transmit and a receive antenna, known as the channel, introduces a fading effect to the transmitted information signal. Thus, this fading path decreases the received power of the information signal and degrades the received signal-to-noise ratio (SNR), which corresponds to the ratio of the received signal power to the noise power. When the received SNR falls below a certain threshold, the received signal can no longer be decoded, and the transmitted information is lost, which is called the deep fade situation. When multiple independent fading channels are used through multiple antennas in a MIMO system, the probability of all links experiencing deep fade is considerably reduced. Hence, the reliability of the transmission improves, which is called spatial diversity gain. Spatial diversity is an effective strategy for dealing with the deteriorating effects of fading channels. Utilizing multiple antennas at the receiver side enables constructively combining the received signals, thereby boosting the received SNR, corresponding to receive diversity. Receive diversity linearly increases with the number of receive antennas. On the other hand, deploying multiple transmit antennas is insufficient to bring transmit diversity into the system. Transmit diversity necessitates either the extension to the time domain along with the spatial domain, known as the space-time coding (STC), or pre-processing of transmit signals utilizing channel state information (CSI) [13]. CSI of a transmission link is the complex channel element that is multiplied by the information signal during the transmission.

Spatial Multiplexing Gain

As an alternative to delivering the same information across multiple links for improving reliability, transmitting separate information signals over distinct channels boosts the data transmission rate without incurring additional transmit power or bandwidth costs. Since all antennas operate in the same frequency band, the amount of transmitting data rises linearly with the minimum of \(N_{T}\) and \(N_{R}\) without requiring an increase in bandwidth, called spatial multiplexing gain [13].

The benefits of MIMO systems can be exploited in multi-user (MU) scenarios by simultaneously serving multiple users at the same time and frequency resource, as illustrated in Fig. 5.

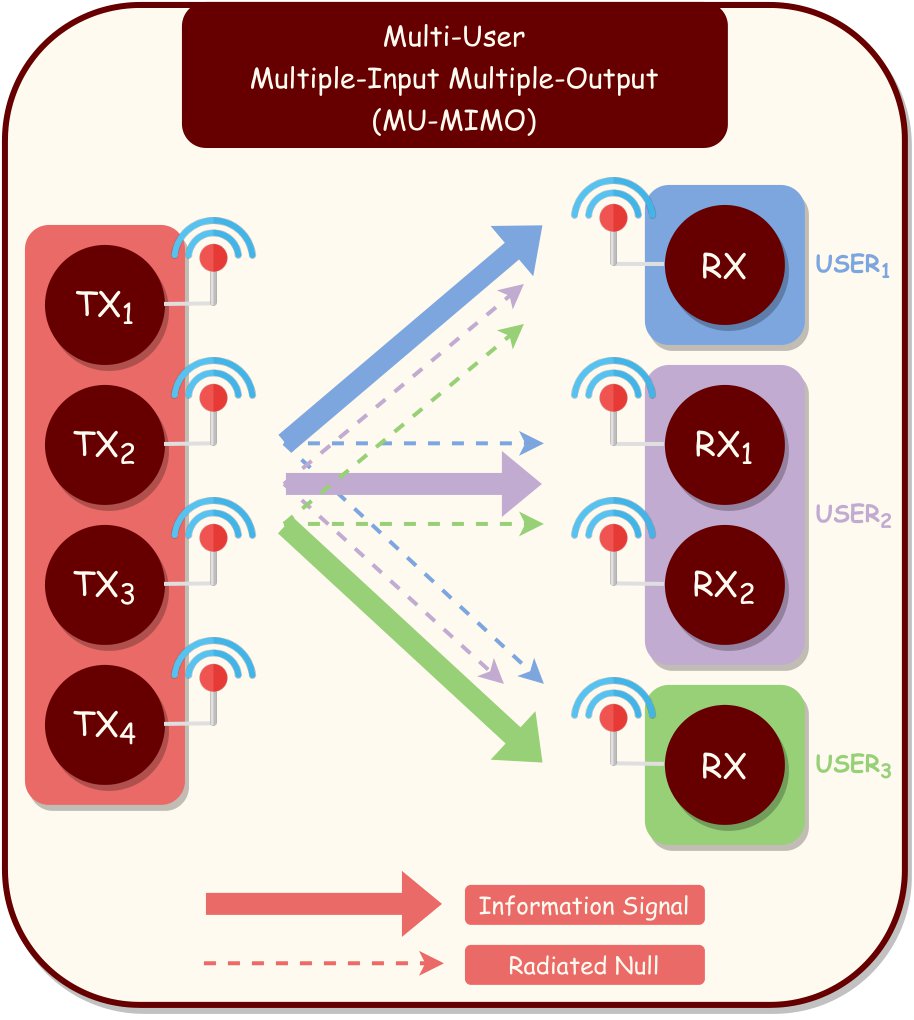
The individual information signal of each user is separately pre-processed using the corresponding CSI and weight matrix prior to the transmission, also known as transmit precoding. Transmit precoding steers each information signal to the appropriate user, maximizing received signal power at each user, called spatial beamforming, while mitigating signal interference between users by radiating null to other users, as demonstrated in Fig. 5. This procedure is called MU interference cancellation. Furthermore, transmit precoding eliminates the fading effect of the channel, which removes the CSI requirement for users [8].

As previously stated, wireless connectivity of IoT devices has been rising, and fascinating applications will emerge at the price of compelling requirements with 6G. The expectations beyond 2030 are extremely high data rates, ultra-low latency, intelligent resource allocation for efficient spectrum utilization in congested areas, enormous energy efficiency, and excellent security algorithms to avoid blocking and jamming attacks [14]. The limited amount of antennas in conventional MU-MIMO systems is insufficient to satisfy the necessities of next-generation wireless communications. Thus, massive MIMO, also known as large-scale MIMO, emerges as a game-changing technology with an excessive number of antennas. In fact, a 5G base station (BS), abbreviated as gNodeB or gNB, in a massive MIMO system is expected to have a few hundred antennas, which is considerably higher than the upper limit, 64, of a 4G base station, called eNodeB or eNB [8], [15]. The most striking aspect of massive MIMO is its extraordinary spatial multiplexing capability through a vast amount of antennas, which improves capacity by at least tenfold [16].

Furthermore, massive MIMO delivers remarkable radiated energy efficiency with a sharp beamforming technique. It should be noted that the radiated energy efficiency is different from the energy costs associated with the deployment process of massive MIMO systems. In particular, radiated energy efficiency refers to how well the users utilize the total transmit power. A large number of transmit antennas and a simple linear precoding technique enable the transmitted energy to be constructively steered into users with incredible precision. In addition, a user’s information signal is canceled when traveling across other users’ channels due to the transmit precoding. Thus, MU interference is mitigated, enhancing the efficiency of radiated energy [16].

Moreover, large-scale MIMO systems in 5G provide tremendous spectral efficiency by simultaneously delivering information to many more users in the same frequency resource compared to the existing 4G technology. The simultaneous service of massive MIMO is especially beneficial at frequencies below 6 GHz, where the frequency spectrum is limited. In a frequency band below 6 GHz, each user can enjoy the entire bandwidth rather than dividing the band for users since massive MIMO can spatially multiplex the users, which improves spectrum utilization [8].

The aforementioned advantages demonstrate that massive MIMO systems exhibit a vast potential to be deployed in 5G and beyond wireless communication technologies. When challenging requirements of the fully-intelligent wireless world of beyond 2030 are considered, massive MIMO systems will play a huge role in the development of extremely fast, energy- and spectrum-efficient, and high-secure cellular networks with ultra-low latency [16].

The next section will explore the fundamental flaws of current massive MIMO technology and investigate the possible use of DL approaches in resolving these drawbacks to truly realize the benefits of massive MIMO systems.

Deep Learning in Massive MIMO

Even though massive MIMO systems show grand promise for next-generation cellular communications, technical constraints restrict the full potential of large-scale antenna arrays [15]. Therefore, it is critical to identify these open research problems and develop solutions for the complete utilization of the massive MIMO technology. As discussed before, the application of DL has been regarded as a promising answer to difficulties in PHY communications. Thus, interest in various DL techniques to address the stated drawbacks in massive MIMO systems has been growing excessively [11]. The primary goal of this section is to highlight the most crucial research problems and how to overcome them with the aid of DL approaches. We divide the issues with the receiver and transmitter sides of a massive MIMO system as follows:

Open Research Problems: Massive MIMO Receiver

The capacity of enormous spatial multiplexing, which boosts data transmission rate, and precise beamforming, which improves radiated energy efficiency and transmission reliability, are two of the most prominent advantages of the massive MIMO technology. However, these notable advancements require high-precision channel estimation to implement precoding properly. In the conventional downlink MIMO system of the current 4G technology, the BS transmits a pilot sequence to users for channel estimation. The transmitted pilot sequence is specially designed and is well-known to users. Consequently, users can examine the received pilot sequence and understand the change in the original pilot sequence caused by the channel, which results in the estimation of channel components. Users send back the estimated channels to the BS for the transmit precoding. Since the pilot sequence includes a pilot symbol for each transmit antenna at the BS, the described procedure is appropriate for the moderate number of antennas in 4G. However, this method necessitates the transmission and feedback of a few hundred pilot symbols for all BS transmit antennas in a massive MIMO system. Furthermore, the pilot symbols should be orthogonal, allowing users to receive each pilot symbol and estimate the corresponding channel individually. Orthogonality can be achieved by either transmitting pilot symbols in different time slots, which takes a long time for the whole sequence and reduces time efficiency, or allocating a frequency band for each pilot symbol, which decreases spectrum efficiency. Therefore, a reliable channel estimation method with a reduced pilot requirement is a critical prerequisite for massive MIMO systems to reach their full potential [1], [16].

DL approaches are expected to allow performing accurate massive MIMO channel estimation while decreasing the number of pilot symbols necessary for an acceptable level of resource use. The extensive literature review in [1] demonstrates that it is even possible to predict the channel using DL methods without transmitting any pilot symbol, which is a significant achievement for large-scale MIMO systems. Furthermore, the traditional channel estimation procedure in 4G assumes a reciprocal channel for MIMO systems, where uplink and downlink channels are identical. When uplink and downlink channels differ, DL techniques relax the reciprocity requirement, allowing for the prediction of uplink channels from downlink channels and vice versa. Another promising improvement introduced by DL techniques is robust channel estimation using low-resolution analog-to-digital converters (ADCs). Since an ADC converts incoming analog signals into digital symbols by quantizing them, the greater the resolution of the ADC, the higher the precision in quantization. On the other hand, increasing the resolution enhances the system’s expenses. Hence, it is also critical to have accurate channel estimation with low-resolution ADCs, even with 1-bit quantization [1].

The next major issue with massive MIMO receivers is the symbol decoding process. The optimal detector in the literature is the maximum likelihood detector (MLD), which searches over all possible transmit symbol vectors to decode the transmitted symbol. This brute force technique brings an unreasonable level of complexity into the system by increasing the processing time. In order to provide a better understanding of the MLD complexity, we might consider a gNB with 128 transmit antennas and a signal set including quadrature phase-shift keying (QPSK) information symbols. It is worth noting that QPSK symbols are generated by modulating the phase of a baseband carrier signal. As QPSK modulation has four levels, MLD scans for four symbols for each transmit antenna. Hence, there are a total of \(4^{128}\) transmit symbol vector combinations, which is greater than \(10^{77}\). Even with a moderate modulation level, the MLD complexity reaches ridiculous levels in a massive MIMO detection. On the other hand, despite significantly less complexity, the alternative linear detectors in the literature, such as zero-forcing (ZF) and minimum mean-squared error (MMSE) detectors, achieve low detection reliability and, as a result, high bit error rate (BER). In addition, these linear detectors have a stringent constraint of \((N_{R} \geq N_{T})\), which is impractical in massive MIMO systems since it is impossible to equip mobile users with more antennas than gNB. As a consequence, it is indispensable to develop a robust symbol detection algorithm capable of overcoming the trade-off between decoding complexity and BER performance [1].

The primary objective of DL-based massive MIMO detectors is to attain near-MLD BER performance while maintaining low computational complexity. DL-based massive MIMO detectors in the literature yield that near-MLD BER performance is achievable with considerably reduced detection complexity through NNs. The learnable parameters of NNs can effectively create a mapping from received symbols to transmitted symbols under perfect CSI assumption. Further improvements eliminate the dependency on perfect CSI and combine the channel estimation and symbol detection operations of a massive MIMO system. Therefore, DL approaches enable direct mapping from received symbols to transmitted symbols, and thus information bits, without the need for extra signal processing.

The completely intelligent receiver framework is the first milestone in DL-aided massive MIMO systems.

Open Research Problems: Massive MIMO Transmitter

As discussed in the previous section, transmit precoding is a vital operation in massive MIMO for three reasons:

• Beamforming information symbols toward users for higher radiated energy efficiency
• Mitigating the fading channel effect for improving the symbol detection reliability
• Ensuring MU interference cancellation for serving many users simultaneously

However, constructing a high-precision precoding matrix in current standards necessitates the use of high-resolution digital-to-analog converters (DACs). Similar to ADCs in the massive MIMO receiver, the higher the DAC resolution, the greater the processing complexity. As a result, cost-friendly massive MIMO systems require the capability to operate precoding with low-resolution DACs reliably [1].

DL-based massive MIMO transmitters replace computationally burdened high-resolution precoding blocks with NNs to offer robust pre-processing of information symbols with incredibly lower complexity. According to the intelligent massive MIMO transmitter literature, even one-bit DL-based precoding can successfully execute pre-processing and ensure the above three properties [1].

Since the birth of wireless communications, conventional PHY architectures have been utilizing mathematically optimized modulation schemes. When information bits are transmitted via the carrier signal phase, bits are said to be PSK modulated. For instance, the possible phase angles for a modulation level of two, called binary PSK (BPSK), are 0 and $latex\pi$ radians. Therefore, the symbol set (constellation) of BPSK modulation includes two symbols: -1 and 1, corresponding to 0 and 1 bits, respectively. For the general case, a modulation order of \(M\), where \(M\) is a power of two, yields the following \(M\)-ary phase angle array: \(\{0, 2 \pi / M, \dots, (2M – 2) \pi / M\}\), each of which corresponding to a separate \(\log_{2}(M)\) bits. As only the phase of a PSK-modulated carrier signal is altered, the carrier signal has the same unit amplitude for all phase angles. Thus, the symbols in a PSK modulation’s constellation are uniformly spaced on the unit circle. Another prominent modulation technique is quadrature amplitude modulation (QAM), in which both the phase and amplitude of a carrier signal convey information symbols. For a square lattice \(M\)-QAM constellation, such as 16-QAM and 64-QAM, the two-dimensional representation of a symbol is: \((A_{I}, A_{Q})\), where \(A_{I}, A_{Q} \in {(1-\sqrt{M}), (3-\sqrt{M}), \dots, (\sqrt{M}-1)}\). Fig. 6 illustrates examples of QPSK and 16-QAM constellations. Although the decision boundaries of these traditional constellation designs are optimized, DL-based MIMO transmitters are anticipated to create unique-shaped constellations adaptable to various transmission environments [1], [17].

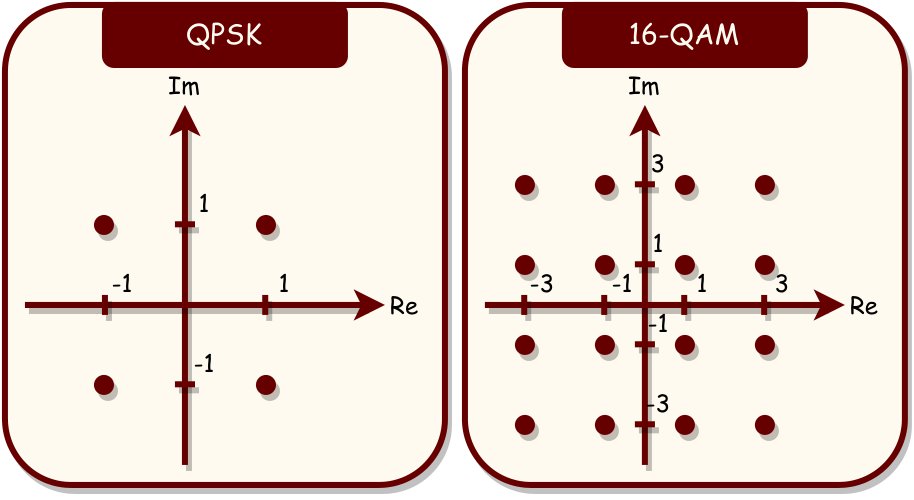
When a DL model is aware of the properties of the transmission environment, the learnable parameters of this model can determine the best locations for constellation symbols and optimize the decision boundaries of these symbols for the given specific environment, potentially improving BER performance over traditional constellations. Nevertheless, the decoding process at the receiver end requires perfect knowledge of the unique transmit constellation. Hence, conventional detectors, such as the MLD and ZF detectors, are incapable of performing reliable detection. Consequently, DL-based massive MIMO transmitters and receivers should collaborate to unlock the full potential of DL approaches, which brings us to the most fantastic concept of future wireless communications: E2E learning [1], [18].

The second breakthrough within the context of DL-based massive MIMO systems is the fully intelligent transmitter architecture.

The Revolutionary Aspiration: End-to-End Learning

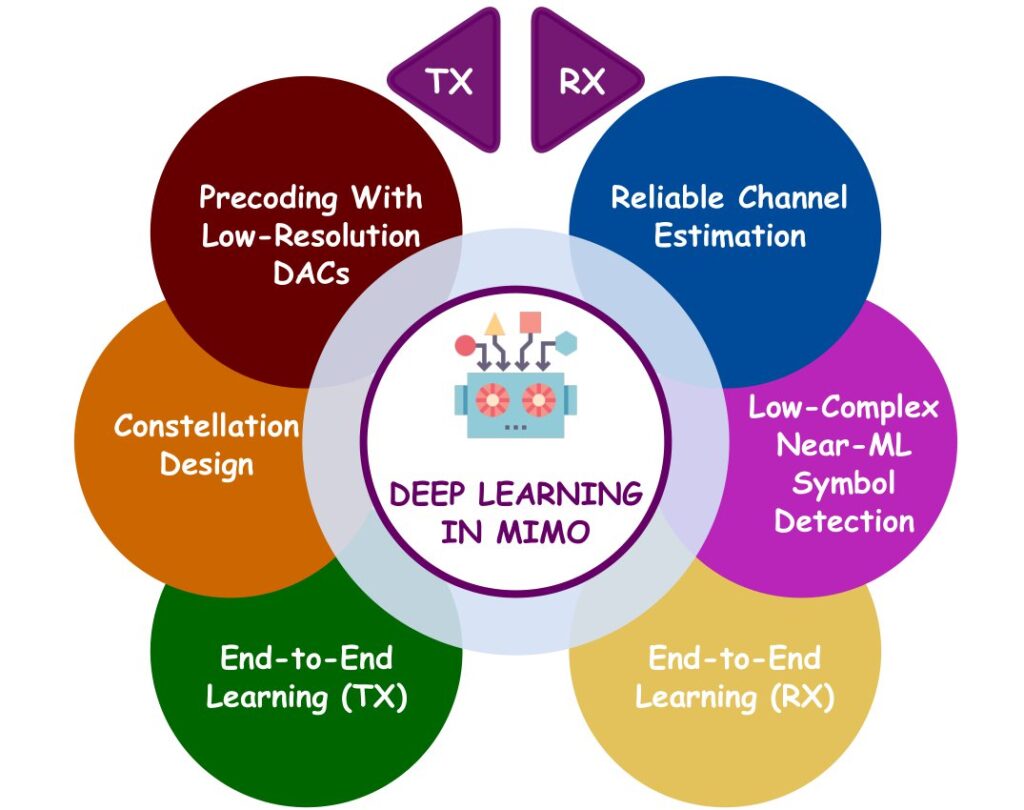
Thus far, we have highlighted the primary constraints of massive MIMO systems that are challenging to address with conventional theoretically optimized signal processing techniques. As the mathematical model-based signal processing blocks of traditional PHY architectures struggle to leverage the full power of massive MIMO, DL techniques have gone mainstream. Even though DL approaches have made significant progress in improving separate signal processing blocks, we are still left with the critical question of whether separate optimization corresponds to overall optimization. As an answer, we are heading into the area of entirely E2E learning, in which a single giant data-based DL network will replace separate model-based signal processing blocks to ensure E2E optimization. This approach will remove the mathematical channel model requirement at both ends, which enhances the practicability since it might be problematic to precisely define the channel model in complicated environments. Fig. 7 depicts the essential applications of DL approaches in transmitter and receiver ends of large-scale MIMO systems.

Conclusion and Future Directions

Massive MIMO technology will undoubtedly have a significant impact on shaping future wireless communication technologies. Massive MIMO systems’ substantial spectrum and radiated energy efficiency, ultra-low latency, robust PHY security, and extreme data rates will make 6G the true facilitator of IoE services. However, the limitations of existing model-based signal processing techniques prohibit massive MIMO technology from reaching its maximum capabilities. Therefore, DL approaches appear as a glaring solution to the shortcomings of massive MIMO by substituting theoretical models with data-based NNs. The eventual goal with data-based PHY architectures is to enable thorough E2E learning, resulting in the E2E optimization of PHY communications.

In this article, we have elucidated the significant advantages of massive MIMO systems along with providing fundamental concepts of PHY communications to aid better understanding. Furthermore, we have studied how DL techniques can overcome the restrictions of current signal processing techniques in massive MIMO technology. Despite the tremendous acceleration in 6G research, we believe that the real wireless revolution is still a long way off. We have identified the following research directions to improve DL-based massive MIMO systems:

• Constructing benchmark real-world channel datasets
• MU E2E communication systems

References

[1] B. Ozpoyraz, A. T. Dogukan, Y. Gevez, U. Altun and E. Basar, “Deep Learning-Aided 6G Wireless Networks: A Comprehensive Survey of Revolutionary PHY Architectures,” in IEEE Open J. of the Commun. Soc., vol. 3, pp. 1749-1809, 2022, doi: 10.1109/OJCOMS.2022.3210648. [Link]

[2] “Release 15,” Mar. 2017. [Link]

[3] L. S. Vailshery, “Number of internet of things (IoT) connected devices world-wide from 2019 to 2030,” Mar. 2022. [Link]

[4] I.F. Akyildiz, S. Nie, S.-C. Lin, and M. Chandrasekaran, “5G roadmap: 10 key enabling technologies,” Comput. Netw., vol. 106, pp. 17-48, Sep. 2016. [Link]

[5] M. Series, “IMT vision-framework and overall objectives of the future development of IMT for 2020 and beyond,” Recommendation ITU, vol. 2083, p. 21, Sep. 2015. [Link]

[6] G. M. B. Series, “Emerging trends in 5G / IMT2020,” Sep. 2016. [Link]

[7] W. Saad, M. Bennis, and M. Chen, “A vision of 6G wireless systems: Applications, trends, technologies, and open research problems,” IEEE Netw., vol. 34, pp. 134-142, Oct. 2020. [Link]

[8] N. Instruments, “5G new radio: Introduction to the physical layer,” Jun. 2018 [Link]

[9] E. Team, “What is the PHY layer,” May 2021. [Link]

[10] ETSI, “5G; NR; physical layer; general description (3GPP TS 38.201 version 15.0.0 release 15),” Sep. 2018. [Link]

[11] T. Wang, C.-K. Wen, H. Wang, F. Gao, T. Jiang, and S. Jin, “Deep learning for wireless physical layer: Opportunities and challenges,” ArXiv, vol. abs/1710.05312, Oct. 2017. [Link]

[12] C.-X. Wang, F. Haider, X. Gao, X.-H. You, Y. Yang, D. Yuan, H. M. Aggoune, H. Haas, S. Fletcher, and E. Hepsaydir, “Cellular architecture and key technologies for 5G wireless communications networks,” IEEE Commun. Mag., vol. 52, pp. 122-130, Feb. 2014. [Link]

[13] A. Paulraj, D. Gore, R. Nabar, and H. Bolcskei, “An overview of MIMO communications – A key to gigabit wireless,” Proc. of the IEEE, vol. 92, pp. 198-218, Nov. 2004. [Link]

[14] J. Zhang, E. Björnson, M. Matthaiou, D. W. K. Ng, H. Yang, and D. J. Love, “Prospective multiple antenna technologies for beyond 5G,” IEEE J. on Sel. Areas in Commun., vol. 38, pp. 1637-1660, Jun. 2020. [Link]

[15] R. Annaswamy et al., “IEEE 5G and beyond technology roadmap white paper,” p. 39, Oct. 2017. [Link]

[16] E. G. Larsson, O. Edfors, F. Tufvesson, and T. L. Marzetta, “Massive MIMO for next generation wireless systems,” IEEE Commun. Mag., vol. 52, pp. 186-195, Feb. 2014. [Link]

[17] M. J. López-Morales, K. Chen-Hu, and A. G. Armada, “A survey about deep learning for constellation design in communications,” in 2020 12th Int. Symp. on Commun. Syst., Netw. and Digital Signal Process. (CSNDSP), pp. 1-5, Jul. 2020. [Link]

[18] F. A. Aoudia and J. Hoydis, “End-to-end learning of communications systems without a channel model,” in 2018 52nd Asilomar Conf. on Signals, Syst., Comput., pp. 298-303, Oct. 2018. [Link]